Teaching Angle Relationships in 8th Grade Math
Angle relationships are one of the geometry topics 8th graders learn. Most students have been exposed to angle measures in previous grade levels, but they learn new concepts including interior angle sums and parallel lines cut by a transversal. Let’s discuss why angle relationships are an important concept to learn, and tips for teaching angles in a limited timeframe.
Some teachers may wonder if angles are a topic we can skip if pressed for time. Afterall, angles only have one standard in eighth grade (depending on your location). However, understanding angles is one of the most important skills needed to be successful in high school geometry. Laying a strong foundation with angles sets students up for success with triangle theorems, arc and circle theorems, and trigonometry. Angles are also relevant to everyday life and careers involving design, carpentry, architecture, engineering, and more.
Teaching angles to 8th graders can be an opportunity for hands-on learning, exploration, and real world connections. So let’s talk about how to approach your angle relationships unit.
Start with the basics.
Geometry topics often get rushed (or even missed), so it’s common for 8th graders to lack basic understanding when it comes to angles. A day of using a protractor will pay off in the long run, especially if students have never used one before. Be sure students understand that a degree measures the openness of angle (and not how big or small the rays appear to be).
Suggestions for basic angle activities:
Measure angles using a protractor.
Ask students to use their arms to (approximately) show different angle measures.
Use this Angle Measure Review for a quick refresh.
For an in-depth lesson on using a protractor, estimating angle measures, and measuring angles, check out this Angle Detective activity.
Teach new angle concepts through hands-on exploration.
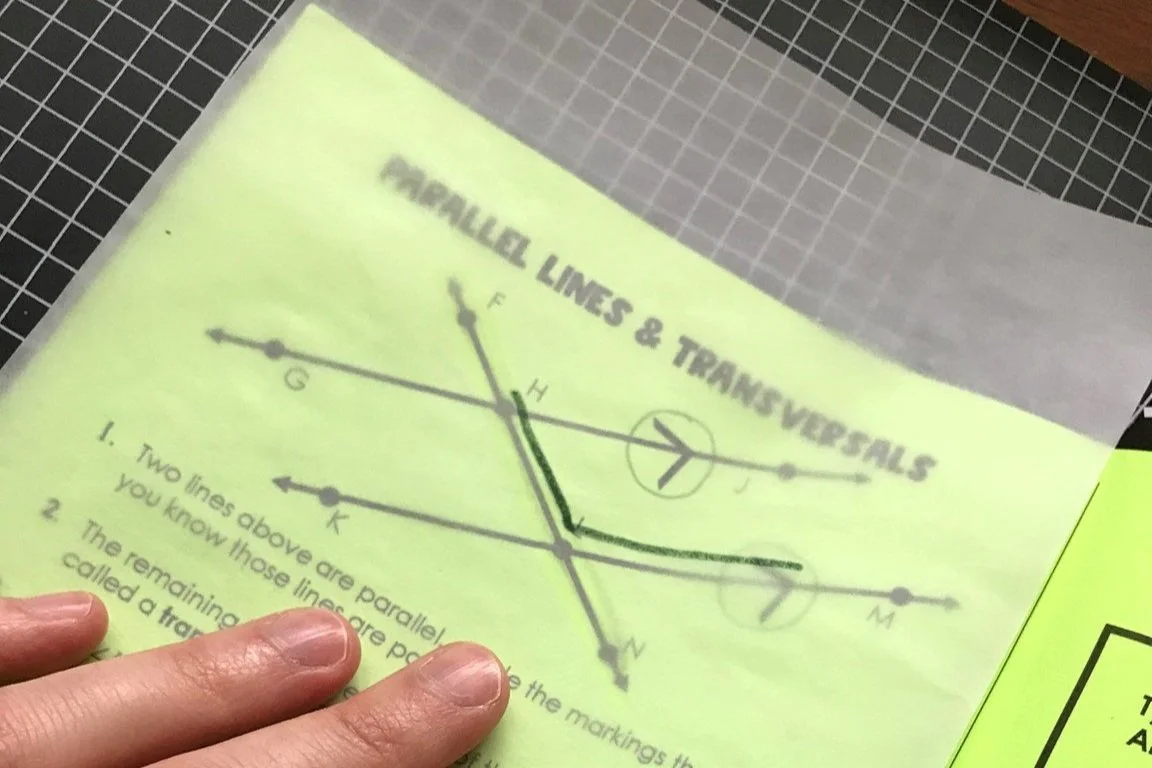
Geometry standards are often opportunities for students to try hands-on experiments. Instead of asking students to memorize formulas (which they often forget), ask students to discover the relationships for themselves. The angle relationships that form with two parallel lines are cut by a transversal can be explored using tracing paper. Students can trace the angles and move them around to find other angles that are congruent or supplementary. The Triangle Angle Sum Theorem can be discovered by cutting the vertices of a triangle and arranging it in a straight line.
When we give students hands-on discovery lessons, they are more engaged. They have to think, reason, and make sense of the math. They are more likely to remember what they discover than if we had just given them notes to study.
For a hands-on exploration of different angle relationships, check out this Angle Discovery Booklet.
Create a word wall with angle visuals.
When we teach angle relationships, we introduce several new vocabulary words. Be sure to help students break apart terms like “alternate exterior angles” to make sense of each word and what it refers to in a diagram.
When it’s time to practice, you may find students constantly getting stuck because they have forgotten or are confusing the vocabulary. A wall with large visuals can help students become familiar with the terms. Instead of coming to the teacher over and over, they can refer to the wall of angle vocabulary. For a set of angle relationship posters that are easy to print and hang, click here.
Make real world connections.
Angles are very relevant to real world scenarios, even if students do not realize it. By including real world angle problems, we can help students see how useful angle relationships are. One example of a real world application for angles is in furniture design. Check out this activity for vertical and supplementary angles, and students love this activity for parallel lines cut by a transversal.
Include unsolvable angle problems.
This tip may sound strange, but let’s think about it. To truly understand angle relationships, students must know when an angle relationship exists. They need to be able to determine if enough information has been provided to find missing angles. Many times they get so focused on calculating, they forget to check if the angle relationship exists.